Calibration of a C-O-C-C Karplus curve for use in oligosaccharide conformational analysis

Roland Stenutz^a, Bidisha Bose^a, Shikai Zhao^b, Francis Cloran^a, Brian Hertz^a, Ian Carmichael^c, Gail Bondo^b, Paul Bondo^b and Anthony S. Serianni^a*

(a) Department of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN, USA 46556
(b) Omicron Biochemicals, Inc., 1347 N. Ironwood Drive, South Bend, IN, USA 46615
(c) Radiation Laboratory, University of Notre Dame, Notre Dame, IN, USA 46556

Introduction

The three-dimensional shape of oligosaccharides is largely determined by the torsions about their glycosidic linkages. Traditionally NOEs have been used to assess conformation, but often only a few are observed due to the "extended" structures of these molecules. More recently trans-O-glycosidic C-O-C-H couplings have gained popularity but they too are insufficient to define conformation unequivocally if substantial flexibility exists. The use of trans-O-glycosidic ¹³C-¹³C couplings [1] can provide additional information. Sometimes, as in the case of ketosides, they are required if an analysis based on coupling constants is to be attempted.

Experimental

The torsional dependence of ²J_COC has been reported [2,3]; herein we present a preliminary Karplus equation for ³J_COCC derived from experimental and calculated couplings for a wide range of model compounds [4]. All experimental data was obtained by direct measurement of the splitting in 1-D ¹³C-NMR spectra recorded at 150 MHz of selectively labeled compounds. Ab initio calculations were performed with a modified version of the GAUSSIAN 94 program using the UB3LYP/6-31G* basis set and Density Functional Theory (DFT) to account for electron correlation effects. The Fermi-contact contribution to the scalar coupling constants were calculated using the finite perturbation method and scaled by +10%.

Scheme 1
	AOCC-pathway
	CAOC-pathway
The two most common coupling pathways

There are several factors known to affect the magnitude of coupling constants (scheme 2). To make reliable predictions of coupling constants all of these effects have to be evaluated . We have looked at two different pathways of interest in the determination of the glycosidic torsions (scheme 1).

Scheme 2

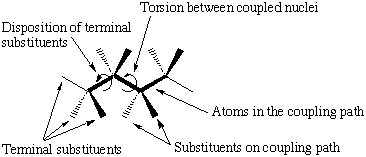Factors affecting the size of three bond coupling constants

The A-O-C-C pathway

A suitable model for the A-O-C-C coupling is the C1-C6 coupling in aldohexopyranoses which provides experimental data for the trans orientation. As can be seen in scheme 3 the size of the coupling constant depends not only on the torsion angle C1-O5-C5-C6 (which is ~180° in all the compounds) but also on the orientation of the anomeric (O-1) and O-6 oxygens. There is an increase by ~0.6-0.7 Hz for each "in-plane" oxygen.
When there is free rotation around the C5-C6 bond the galactopyranoses (4a,b) have a ~0.3 Hz larger C1-C6 coupling than the glucopyranoses (3a,b) because of enhancement by the presence of 40% tg rotamer [5] (scheme 4) which places O6 in-plane. 6-deoxy-glucose (5a,b) behaves just like glucose, i.e. the presence of an oxygen makes no contribution to the coupling if it is gauche to the coupling path.

Scheme 3

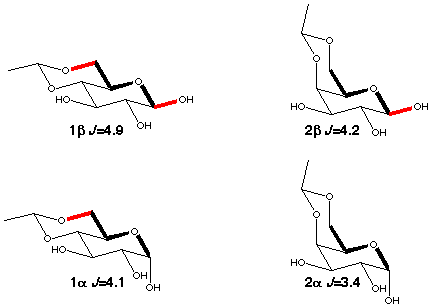Scheme 4

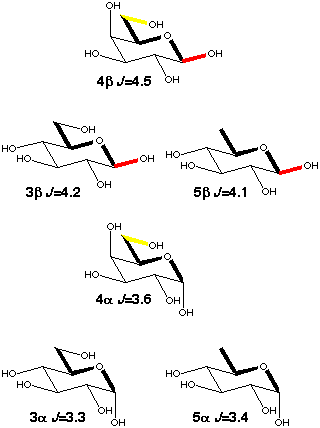Models for the gauche couplings are more difficult to find. Couplings in five or six membered rings can not be used since they have dual pathways (²⁺³J and ³⁺³J respectively). However the C1-O5-C5-C6 coupling in 3,6-anhydro-glucosides (6a,b scheme 5) are suitable models. The difference in coupling between the a and b anomers shows that the in-plane effect is approximately the same size as in the trans arrangement.

Scheme 5

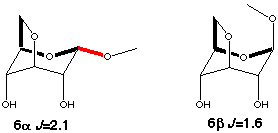The C-A-O-C pathway

The trans conformation of the C-A-O-C pathway can be modeled by the C1-C2-O6-C6 coupling in ketohexoses. Obtaining the value for the coupling without any enhancement is straight forward as the orientation of the exocyclic hydroxymethyl groups in 7b, 8a and 9b will avoid the conformation with an in-plane oxygen be cause of 1,3-diaxial interactions. A lower limit of 0.7 Hz for the in-plane effect can be determined from 9a which can assume both in-plane and out-of-plane orientations. To determine this value more accurately model compounds with fixed exocyclic torsions will be needed.

Scheme 6

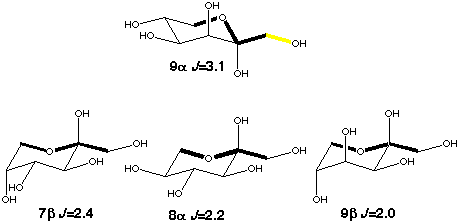The gauche conformation was modeled using the C2-C1-O1-C1' coupling in ethyl aldosides (10a,b, 11a,b). Their conformation is determined mainly be the exoanomeric effect which favors a +60° torsion angle. An in-plane effect is present only in the α-D-mannoside (11a) and the observed enhancement is again ~0.7 Hz.
Contrary to expectation the experimental data seems to suggest a larger coupling in the gauche conformation than in trans. This is at variance with the results from ab initio calculations which give similar couplings for the A-O-C-C and C-A-O-C pathways. All of the model compounds for this coupling pathway are flexible and may therefore be compromised as models. The in-plane effect appears to be the same as in the A-O-C-C pathway.

Scheme 7

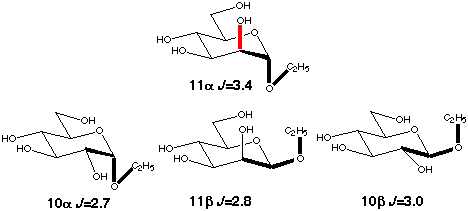Karplus Curve

An approximate Karplus curve (figure 1) was fitted to the experimental and computed data (excluding ketoses and structures with in-plane effects). Both C-A-O-C and A-O-C-C data were fitted to the same curve since computational results indicate that they are very similar. Since there is very little data for small angles and data suggests that the coupling constants for 0° and 180° are very similar no cosine term was included in equation 1.

Equation 1	³J_CCOC=3.49cos²θ+0.16
Equation 2	³J_CCOC=2.24cos²θ-1.3cosθ+0.5

This equation differs from that of Xu & Bush [6] (equation 2) in the region below 90° where it predicts larger couplings.
To obtain the correct coupling from equation 1, an adjustment of 0.7 Hz must be added for each in-plane effect.

Figure 1
Karplus curve for ³J_COCC

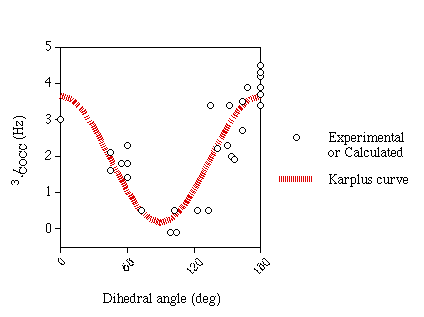Summary

³J_COCC magnitude depends not only on the C-O-C-C torsion angle but also on the orientation of electronegative substituents on the terminal coupled carbons. The effect of a terminal in-plane oxygen is ~+0.7 Hz and is additive. There is no substituent effect for out-of-plane terminal substituents. Despite the large number of model compounds only the trans couplings of the A-O-C-C pathway is well described. Ab initio calculations are the most promising way to complement the available data because of the difficulties in preparing suitable labeled compounds for experimental measurements.
Several specifically ¹³C-labeled disaccharides are now being prepared using chemical and enzymatic (glycosidase) methods in order to investigate their conformational properties using this new equation and computational (MO, MD) methods.

Acknowledgments

This work was supported by a grant from Omicron Biochemicals, Inc., of South Bend, Indiana. R.S. wishes to thank Knut och Alice Wallenbergs Stiftelse for financial support.

References

(a) Hayes, M.L.; Serianni, A.S.; Barker, R.; Carbohydr. Res. 100, 87-101 (1982).
(b) Duker, J.M.; Serianni, A.S.; Carbohydr. Res. 249, 281-303 (1993).
Church, T.; Carmichael, I.; Serianni, A. S.; Carbohydr. Res. 280, 177-186 (1996).
Serianni, A.S.; Bondo, P.B.; Zajicek, J.; J. Magn. Reson. Ser. B 112, 69-74 (1996).
Bose, B.; Zhao, S.; Stenutz, R.; Cloran, F.; Bondo, P.; Bondo, G.; Hertz, B.; Carmichael, I.; Serianni, A.S.; J. Am. Chem. Soc., submitted for publication.
Nishida, Y.; Ohrui, H.; Meguro, H.; Tetrahedron Lett. 25, 1575-1578 (1984).
Xu, Q.; Bush, A.; Carbohydr. Res. 306, 335-339 (1998).
Tvaroska, I.; Hricovíni, M.; Petráková, E.; Carbohydr. Res. 189, 359-362 (1989).
Hirotsu, K.; Shimada, A.; Bull. Chem. Soc. Jpn. 47, 1872-1879 (1974).

Work related items