3. Conformational analysis

3.1 Introduction

The purpose of conformational analysis is to obtain a description of the three-dimensional structure of molecules. Such knowledge is required in order to understand the interactions between molecules, e.g. carbohydrates and proteins, and is also of help in the structure determination by NMR spectroscopy. The conformation of a molecule may be described at different levels of detail. In the simplest case a single conformer, i.e. three-dimensional structure, may be sufficient to explain experimental data. The assumption of a single conformer may however result in a "virtual conformation", i.e. a physically unreasonable structure, if the molecule is flexible. In such cases, data may be better fitted by assuming an equilibrium between several conformers. This approach has the advantage that the physical properties of individual conformers may be approximated directly from suitable model compounds. In some cases a distribution function has been fitted against a few observables so that a continuous, e.g. a Gaussian or maximum entropy distribution, rather than discrete distribution of conformers is obtained. ^27-29 The use of a continous distribution also requires a more detailed understanding of the measured physical properties. Only in a few cases has the influence of flexibility and solvation been addressed, since this requires a large amount of experimental data and long and complex computer simulations.

3.2 Experimental methods

3.2.1 Crystallography ^30-32

From single crystal X-ray diffraction data the coordinates of all atoms can be obtained. Crystallisation can be an obstacle as many carbohydrates do not readily form sufficiently good crystals. If they are microcrystalline they can still produce a powder diffraction pattern, from which, in principle, the same information can be obtained using Monte Carlo methods.^33-35 Starting geometries for the refinement of diffraction data may be obtained from NMR spectroscopy ³⁶ or molecular modelling. ^37,38 Solid state structures can naturally give little information about the flexibility of molecules, although statistical treatments of large collections of similar structures with common fragments can give population distributions similar to those observed in solution (table 3.1). ³⁹

3.2.2 NMR spectroscopy

NMR data is often simpler to obtain than a crystal structure. The amount of structural information that can be gained is however limited as data from NMR spectroscopy is dominated by short range effects. Conformational flexibility may complicate the picture further as conformational changes in general are fast on the NMR time-scale so that only time-averaged properties are observed. Many NMR-parameters have been proposed for conformational analysis but only couplings constants (³J) and nuclear Overhauser effects (NOE) have found wider use. Both homo- and heteronuclear ( ³J_HH, ³J_CH) coupling constants ⁴⁰ are dependent on the size of the torsion angle around the connecting bond. The dependence is described by Karplus type equations ⁴¹ which are reasonably accurate for proton-proton couplings but much less so for carbon-proton couplings. Nuclear Overhauser effects are inversely proportional to the sixth power of the inter-nuclear distance making them sensitive probes for short distances. Relaxation rates, which are dependent on molecular motion, are also often measured but the interpretation of these is difficult since it requires a separation into global and local contributions. ⁴²
As experimental methods improve and more data become available it is likely that new correlations will be discovered and the accuracy of those in current use will improve. Even when NMR data themselves are not sufficient to determine conformational equilibria, useful interpretations can often be made if combined with molecular dynamics simulations, using experimental values as restraints or by comparison with values calculated from simulations. Unlike crystallography, NMR spectroscopy is not an all-or-nothing method. It is always possible to get some information, but seldom sufficient to allow an unambiguous interpretation.

3.3 Computational methods

If it the energy of different conformers is known it should be possible to calculate their relative abundance by Boltzmann weighting. Computational chemistry provides us with such methods based on quantum mechanics and molecular mechanics.
Quantum mechanical methods (ab initio or semi-empirical) solve wavefunctions and have to take both electrons and nuclei into account. This makes the calculations complex and demanding in terms of computer time and therefore their use remains restricted to small systems, often with fixed geometries. Despite these limitations there are calculations which require knowledge about electron densities or excited states, e.g. UV-spectra, that can not be performed in any other way.
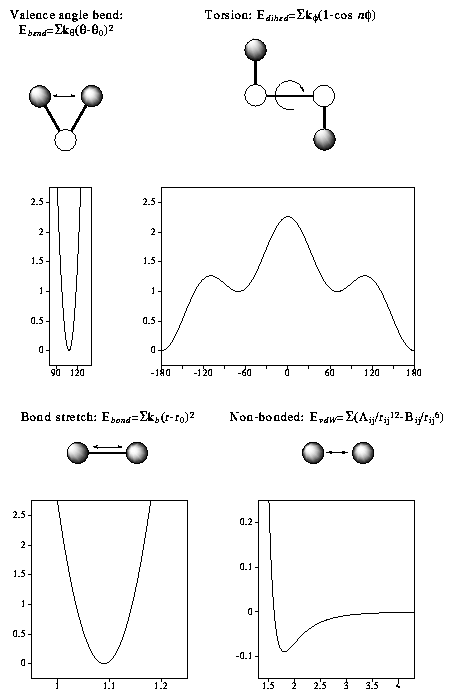
In molecular mechanics (MM) the forces between atoms are approximated by empirical functions. These functions are simple and fast to evaluate and allow the treatment of much larger systems containing hundreds of molecules and thousands of atoms. The total "steric"-energy of a conformer is given by summing the stretch, bend, torsion and non- bonded energy terms which constitute a force field.

Energy terms in a force field

Since the parameters, i.e. the coefficients in the equations, in force fields are empirical their quality relies on the availability of experimental data. Whilst this is not generally a problem for stretch or bend interactions, the parameters for non-bonded interactions and high energy structures are difficult to obtain by experimental methods. Because of these difficulties some recent force fields have been derived from quantum mechanical calculations. ⁴³
There has also been a certain bias towards peptides and nucleotides in most force fields, but there are now special carbohydrate parameters available for most force fields. ^44,45
A simple force field for carbohydrates, which has been used frequently, HSEA, ⁴⁶ uses fixed geometries for the rings of the sugar residues and ignores both hydrogen bonding and electrostatics. Despite these shortcomings it has been found to reproduce experimental data in many cases.
To obtain the structure with lowest energy, and hence the most populated, a geometry optimisation is performed. This is done by moving the atoms until reaching an energy minimum. During such a minimisation it is however not possible to cross energy barriers so that it is never certain that the global energy minimum has been reached. The only way to overcome this problem, referred to as the multiple-minima problem, is to find every possible energy minimum, a task which may be accomplished using grid search or Monte Carlo methods. The energy of isolated molecules does not give a particularly accurate description of the population distributions of actual molecules. A much more realistic model is provided by Metropolis-Monte Carlo ^47,48 (MMC) or molecular dynamics (MD) simulations which, given sufficient time, produce the proper ensembles of structures from which physical properties may be computed. Whilst MMC is a purely statistical method, MD is, in principle, time dependent MM. Instead of minimising the energy of a molecule, all atoms are assigned velocities and then allowed to move under the influence of the force field. Both statistical and dynamic properties are readily extracted from MD.

3.4 Solvent models ^49-51

Since many experiments are performed on molecules in solution it is highly desirable to be able to mimic solvent effects in simulations. This is particularly important for the study of biological interactions which take place in the presence of water. The simplest adjustments are the increase of the dielectric constant or the inclusion of a reaction field, ^52,53 with a dampening of the electrostatic interactions as a result. The inclusion of stochastic forces on atoms to simulate random collisions with solvent molecules (Langevin dynamics) ^54,55 is another method to introduce implicit solvent. When dealing with strongly hydrogen bonding solvents such as water it may be necessary to include explicit solvent molecules around the molecule to properly simulate solute-solvent interactions. Using MD it is important that the simulation is allowed to run for sufficient time so that all allowed conformations are visited several times. If not the results of the simulation are likely to be inaccurate no matter how accurate the model itself may be.

3.5 Application to carbohydrates

The conformation of carbohydrate residues can be divided into that of the ring and that of the exocyclic torsions. In oligosaccharides the two additional degrees of freedom across the glycosidic linkage are also of interest.

**Fig. 3.2:** Degrees of conformational freedom in a saccharide Torsions of interest are indicated in bold

The conformation of the ring is dominated by steric interactions between axial groups. In hexopyranoses this causes a strong preference for the less crowded ⁴C₁ conformation in the D-series (¹C₄ in the L-series) as this places C-6 in an equatorial position. 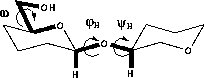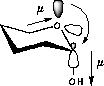In pentoses, furanoses and unsaturated pyranoses the differences in steric energy between conformations are much smaller so that the conformation is often determined by the anomeric effect. The term anomeric effect ^56-61 is used to describe the preference for placing electronegative substituents anti to the electron pair of a heteroatom, i.e. oxygen.

**Fig 3.3:** The anomeric effect
a) Donation of electron density into the C-O bond	b) No overlap of orbitals

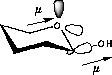
Lower dipolmoment (µ) Favoured by electrostatics	Higher dipolmoment (µ)

The existence of such an effect has been demonstrated in five (furanose), ⁵⁹ six (pyranose) ⁶⁰ and seven-membered ^54,55 rings. The existence of a reverse anomeric effect ⁶² has also been suggested. The anomeric effect has been explained using electrostatic arguments, or molecular orbital interactions. In flexible rings it is often necessary to determine both the structure of the preferred conformers as well as their respective populations. Often a simplified description of the conformations, based on pseudorotation angles and puckering amplitudes ⁶³ is used to make the analysis more manageable. The first attempts to determine the ring conformation of carbohydrates were made by Hassel and Ottar (1947) using X-ray diffraction ⁶⁴ and by Reeves (1950) from the optical rotation of cuprammonium complexes. ⁶⁵
The conformation of the glycosidic linkage is described by two torsions; φ_H (H1-C1-On-Cn, in which n is the linkage atom) and ψ_H (C1-On-Cn-Hn). There is a general preference for a gauche arrangement of the ring oxygen and the anomeric substituent ( φ_H≈+60° for β-D-sugars, -60° for α-D-sugars). This is called the exo-anomeric effect ⁶⁶ and is of similar origin as the anomeric effect. The value of ψ_H is mainly determined by steric effects and is usually -50° to +50°. The conformation around the glycosidic linkage can be determined by measuring ³J_COCH ^67,68 couplings across the linkage.
In hexopyranoses there is one more exocyclic torsion, namely that of the C5-C6 bond. This torsion is described either by the torsion angle, ω, defined as O5-C5-C6-O6, or as one of three possible staggered conformers, gt (ω≈60°), gg (ω≈-60°) or tg (ω≈180°). The conformation distribution is determined by a combination of steric- and stereoelectronic factors. The most important steric factor is the repulsion between the hydroxyl groups in 4- and 6-positions (Hassel-Ottar effect). ⁶⁴ There is a preference for values of ±60° for ω (table 3.1) which has been explained by the gauche effect. ⁶⁹

**Fig. 3.4:** The gauche effect (illustrated for O5-C5-C6-O6)
C-O/C-O orbital overlap	C-O/C-H orbital overlap

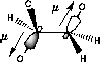
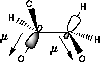
Favoured by electrostatics but has higher total energy	Donation of electron density from the C-H bond into the C-O bond

The gauche effect is caused by the ability of less electronegative substituents to donate electrons into the C-X bond when they are anti. If the assignment of the NMR signals from the prochiral protons on C-6 is known then it is possible to determine the population in the three rotameric states experimentally from the size of the H5-H6 couplings.

**Table 3.1:** Relative populations (P) of hydroxymethyl rotamers as determined by different experimental methods (using three state models)
	Glucose			Galactose
	P_gt	P_gg	P_tg	P_gt	P_gg	P_tg
³J_HH⁷⁰	44	56	0	47	14	39
Crystal structures ³⁹	40	60	0	58	8	34
Optical rotation ⁷¹	75	25	0	66	0	33

Some saccharides, such as the blood group determinants, ⁷² are relatively rigid and the structures obtained by energy minimisations with simple force fields like HSEA are in good agreement with both solution- and solid state structures ⁷³ despite the neglect of electrostatic interactions and solvent. Other saccharides, like sucrose, ^74,75 depend on the inclusion of explicit water to reproduce experimental data. There are recent results showing that both φ_H-⁷⁶ and ψ_H-trans ⁷⁷ conformers can be present in some oligosaccharides, which suggests that the conformational flexibility in solution is greater than previously believed. The large solvent exposed surface area of carbohydrates makes them difficult to model accurately and the experimental data are often insufficient to solve conformational problems. Therefore the conformational analysis of carbohydrates is more difficult than for most other compounds and relies on the combination of experimental and computational methods. ⁷⁸

The structure and conformation of saccharides determined by experiment and simulation