DFT Calculations on disaccharides

DFT Calculations on disaccharides: New Insight into conformation and trans-O-glycosidic spin couplings

Roland Stenutz^a, Francis Cloran^a, Ian Carmichael^b, and Anthony S. Serianni ^a*
^(a)Department of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN, USA 46556
^(b)Radiation Laboratory, University of Notre Dame, Notre Dame, IN, USA 46556

Introduction

To understand the many biological roles of oligosaccharides, a knowledge of their three-dimensional structure is required. One way to gain insight into the conformation of an oligosaccharide is through the measurement of transglycosidic coupling constants. Coupling constants have been shown to depend on the geometry of the molecule, mainly the torsion angle between the coupled nuclei but also bond lengths and bond angles and substitution pattern.
Using ab initio quantum mechanical methods, coupling constants can be calculated. Herein we apply Density Functional Theory (DFT), a quantum mechanical analysis based on electron density, to disaccharide models to optimize their geometries by minimizing the potential energy of the system. From the optimized geometries, J coupling values can be determined by calculating the Fermi-contact component of the indirect spin-spin coupling constant. The accuracy of these Jvalues can be assessed through comparison of the computed J values with experimental data. As the computed J_CH values were somewhat smaller and the J_CC slightly larger than the experimental values, adjustments of +5% and -10% respectively were applied.
In this study, the geometries of some models of β-(1→4) linked disaccharides were optimized as a function of the glycosidic torsion angle, Ψ_H. The geometries were then used to calculate two-bond and three-bond trans-O-glycosidic J couplings to determine the usefulness of Density Functional Theory to the analysis of larger molecular systems, such as disaccharides.

Experimental

All ab initio calculations were performed with a modified version of the GAUSSIAN 94 program using the UB3LYP/6-31G* basis set [6] and Density Functional Theory (DFT) to account for electron correlation effects. The Fermi-contact contribution to the scalar coupling constants were calculated using the finite pertubation method.
The basic disaccharide mimics used in these calculations are shown in Scheme 1.

Scheme 1

The starting geometries of the Φ_H-torsions (H1'-C1'-O4-C4) were set to +60° to give the rotamers stabilized by the exoanomeric effect. The H2'-C2'-O2'-HO2' torsion was arbitraily set to +60° and, when applicable, the C2-C3-O3-HO3 torsion set to 180°. All three staggered rotamers around the Ψ_H torsion (C1'-O4-C4-H4) were optimized but only in the case of compound 1 did this result in two different gauche conformers. In compounds 2, 3 and 4 both gauche (~60°) starting geometries gave the same optimized structure. This is in agreement with results from molecular mechanics/molecular dynamics and NMR which suggest only one "syn" (Ψ_H~0°) geometry with significant flexibility.
On completion of the geometric optimizations, J calculations were performed for the pathways indicated below in Scheme 2.

Scheme 2

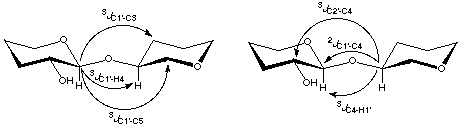
Results and Discussion

Geometry

From the three staggered starting geometries only two final geometries are obtained for compounds 2-4 after geometry optimization: anti (Ψ_H~180°) and syn (Ψ_H~-20°). The values for Ψ_H shown in table 1 depart considerably from the idealized staggered torsion angles of ~60°.

Table 1
Compound	syn (Ψ_H~0°)		anti (Ψ_H~180°)
	Φ_H	Ψ_H	Φ_H	Ψ_H
1^a	+47°	-17°	+32°	+171°
	+43°	+22°
2	+32°	-25°	+18°	+180°
3	+44°	-19°	+52°	-159°
4	+32°	-22°	+17°	-179°
β(1→4)^b	+23° - +60°	-51° - +12°

^a) two syn-structures
^b) range for 35 X-ray structures of β(1→4) linked disaccharides in the Cambridge crystallographic database

It is interesting to note that, in the unsubstituted compound (1), the two gauche rotamers must be separated by an energy barrier since they give different optimized geometries. In all cases, the syn geometry was lower in energy than the anti geometry by 2.4-3.2 kcal/mol. Thus the anti conformation is not necessarily inaccessible but much less favored than the syn conformation.

Trans-O-Glycosidic ²J_COC Values

In the optimized structures the glycosidic ²J_COC were calculated. According to the empirical projection resultant method [4], the size of ²J_COC depends only on Φ_H and should be ~-2 Hz for all the compounds. This is consistent with the results obtained from the Fermi-contact calculations which gave values of -1.9 to -2.5 Hz (average -2.0 Hz). These results encourage the use of DFT for future two-bond glycosidic J coupling analyses.

Trans-O-Glycosidic ³J_COCH Values

There are two glycosidic ³J_COCH of interest. Table 2 lists the computed coupling constants as well as their associated dihedral angles.

Table 2
Calculated Three Bond CH Couplings in Model Disaccharides
Structure		³J_C1'-H4	³J_H1'-C4
1	syn (sc-)	6.1 (-17°)	4.3 (48°)
	syn (sc+)	5.9 (22°)	4.2 (43°)
	anti	8.3 (171°)	4.5 (32°)
2	syn	5.5 (-26°)	5.4 (32°)
	anti	9.0 (180°)	4.6 (18°)
3	syn	6.1 (-19°)	4.5 (44°)
	anti	8.4 (-160°)	2.4 (52°)
4	syn	5.7 (-22°)	5.1 (32°)
	anti	9.0 (-179°)	4.4 (16°)

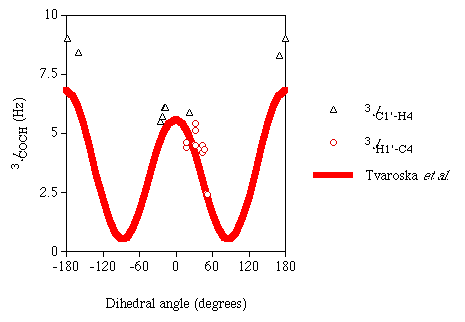
Although not quantitative, these computed J couplings are of the same size as those reported experimentally. It has also been noted that ³J_COCH constants display a Karplus-like dependency on the torsion angle between the coupled atoms. Figure 1 is a plot of the computed J couplings versus their associated dihedral angles. Included in this plot for comparison is an experimentally derived Karplus curve for ³J_COCH reported previously [7].
It is difficult to ascertain whether or not the DFT results support the empirical Karplus relationship of ³J_COCH because of the absence of data for the dihedral angles around ~90°. Efforts are being made to measure theoretical J couplings over the entire torsional range for this three-bond pathway.

Figure 1
Calculated ³J_COCH

Trans-O-Glycosidic ³J_COCC Values

The other ³J of interest across the glycosidic linkage are the three carbon-carbon couplings. Table 3 lists the computed coupling constants as well as their associated dihedral angles between the coupled nuclei.

Table 3
Calculated Three-Bond CC Couplings in Model Disaccharides
Compound		³J_C1'-C3	³J_C1'-C5	³J_C2'-C4
1	syn (sc-)	0.0 (105°)	3.3 (-135°)	3.8 (168°)
	syn (sc+)	2.2 (141°)	0.0 (-99°)	3.4 (164°)
	anti	0.0 (-72°)	1.7 (55°)	3.3 (152°)
2	syn	0.0 (95°)	4.4 (-144°)	3.4 (153°)
	anti	1.0 (-65°)	1.4 (63°)	2.3 (137°)
3	syn	0.0 (102°)	3.6 (-137°)	3.7 (164°)
	anti	3.2 (-42°)	0.0 (86°)	3.7 (172°)
4	syn	0.0 (98°)	3.9 (-140°)	3.3 (153°)
	anti	1.2 (-64°)	1.3 (65°)	2.3 (137°)

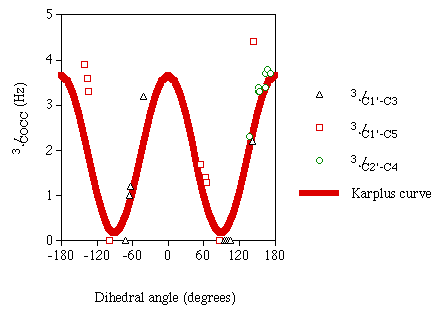
The values for these computed J couplings of similar magnitude as those recently reported experimentally in this laboratory, although not quantitative. As with the ³J_COCH values, magnitudes for ³J_COCC are reported to express a Karplus dependency on the dihedral angle between the two coupled nuclei. Figure 2 is a plot of the computed carbon-carbon couplings versus the associated dihedral angles. Included in this plot is a graph of the idealized empirical Karplus curve for this coupling pathway recently determined in this laboratory [8].

Figure 2
Calculated ³J_COCC

In this plot one can see a Karplus-like dependency of the ³J_COCC values on the associated dihedral angles. In the dihedral angle range of 140° to 170°, a scattering of the data points from an idealized curve is observed. This scattering may be explained by substituent effects (O5 in plane) along the J coupling pathway. If there were substituent effects on the ³J_COCC pathway, which is seen in ³J_HH pathways, one might expect to see these effects amplified on the steeper part of the Karplus curve. Despite these deviations, the computed ³J_COCC show good agreement with the Karplus equation. These results are encouraging and justify future application of DFT to analyze other model disaccharides.

Summary

In the DFT analysis of disaccharide models 2-4 where Ψ_H was initially varied, two optimized geometries were obtained from the three staggered starting geometries: one geometry where Ψ_H was ~180° (anti) and the other geometry where Ψ_H was ~-20° (syn). It was determined in each case that the anti geometry was a higher energy structure than the syn geometry by 2.4-3.2 kcal/mol.
²J_COC couplings across the glycosidic linkage were calculated for all optimized structures. Couplings of approximately -2 Hz were calculated, which is in good agreement with the results of the projection resultant method.
³J_COCH across the glycosidic linkage were calculated for all optimized structures. The ³J_COCH were similar to those measured experimentally [7]. Due to the absence of models with dihedral angles around ~90°, the ³J_COCH couplings could not be used to test the presence of a Karplus relationship in these model structures.
³J_COCC couplings were calculated for all optimized structures. The ³J_COCC were close to those measured experimentally on similar compounds. Despite some scatter for dihedral angles around 180°, the relationship of the ³J_COCC to the associated dihedral angles was in good agreement with an experimental Karplus relationship reported recently for the ³J_COCC pathway [8].

References

Levine, I.N.; Quantum Chemistry; Prentice-Hall, Inc.: Englewood Cliffs, NJ, 1991.
Lebanowski, J.K.; Andzelm, J.W. (eds.);Density Functional Methods in Chemistry; Springer-Verlag: New York, NY, 1991.
Haasnoot, C.A.G.; de Leeuw, F.A.A.M.; Altona, C.; Tetrahedron 36, 2783-2792 (1980).
Church, T.; Carmichael, I.; Serianni, A.S.; Carbohydr. Res. 280, 177-186 (1996).
Carmichael, I. J. Phys. Chem.; 97, 1789-1792 (1993).
Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Gill, P.M.W.; Johnson, B.G.; Robb, M.A.; Cheeseman, J.R.; Keith, T.; Petersson, G.A.; Montgomery, J.A.; Raghavachari, K.; Al-Laham, M.A.; Zakrzewski, V.G.; Ortiz, J.V.; Foresman, J.B.; Peng, C.Y.; Ayala, P.Y.; Chen, W.; Wong, M.W.; Andres, J.L.; Replogle, E.S.; Gomperts, R.; Martin, R.L.; Fox, D.J.; Binkley, J.S.; Defrees, D.J.; Baker, J.; Stewart, J.P.; Head-Gordon, M.; Gonzalez, C.; Pople, J.A.;Gaussian 94, Revision B.3; Gaussian, Inc.: Pittsburgh, PA, 1995.
Tvaroska, I.; Hricovíni, M.; Petráková, E.; Carbohydr. Res. 189, 359-362 (1989).
Bose, B.; Zhao, S.; Stenutz, R.; Cloran, F.; Bondo, P.; Bondo, G.; Hertz, B.; Carmichael, I.; Serianni, A.S.; J. Am. Chem. Soc., submitted for publication.

Work related items

DFT Calculations on disaccharides