The structure and conformation of saccharides determined by experiment and simulation

4 Conformational studies on methyl 6-O-[(R)- and (S)-1-carboxyethyl]-a-D-galactopyranoside

Home :: The structure and conformation of saccharides determined by experiment and simulation :: 4 Conformational studies on methyl 6-O-[(R)- and (S)-1-carboxyethyl]-a-D-galactopyranoside

4.1 Introduction

Butyrivibrio fibrisolvens is an anaerobic bacterial species commonly found in the intestine of herbivorous mammals. The species can be divided into two distinct taxonomic groups depending on the presence or absence of an unusual acidic sugar, 6-O-[(R)-1-carboxyethyl]-D-galactose (1),79 in their extracellular polysaccharide. Another acidic sugar, 4-O-[(S)-1-carboxyethyl]-L-rhamnose,80,81 was present in only one of the strains examined. Sugars substituted with carboxyethyl groups are also produced by some other bacteria.82
Fig. 4.1:The methyl glycosides of the two naturally occurring carboxyethyl sugars
methyl 6-O-[(R) -1-carboxyethyl] -α-D-galactopyranside (1) methyl 4-O-[(S) -1-carboxyethyl] -α-L-rhamnopyranoside
methyl 6-O-[(R)-1-carboxyethyl]-a-D-galactopyranside methyl 4-O-[(S)-1-carboxyethyl]-a-L-rhamnopyranoside
In order to determine the configuration of the carboxyethyl group it was necessary to synthesise reference compounds of known absolute configuration which then could be used for comparison with the native material. A method based on the formation of a rigid lactone with the carboxyethyl group has been proposed.83,84
The relative configuration of the carboxyethyl group can then be determined by NOE measurements. As methyl glycosides are preferable for the spectroscopic studies and allow a direct comparison with native polysaccharides we chose to prepare them rather than the free sugars 85 or carboxyl reduced derivatives.86

4.2 Preparation of carboxyethyl sugars

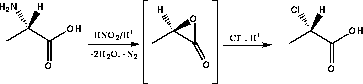
Alkylation of sugar derivatives with optically pure α-chloropropionic acid had been reported previously in connection with the synthesis of 2-amino-3-O-[(R)-1-carboxyethyl]-2-deoxy-D-glucose (muramic acid) 87 and 3-O-(1-carboxyethyl)-L-rhamnose.85 By this approach the separation of diastereomers was avoided.
The (R)- and (S)-α-chloropropionic acids 88 were prepared by diazotation of (R)- and (S)-alanine respectively in 3M HCl. Initially the highly strained α-lactone of lactic acid is formed which is opened by chloride ion to give chloropropionic acid with overall retention of configuration.
Scheme 4.1
Preparation of 2-chloropropanoic acid
Alkylation of the galactose derivatives with α-chloropropionic acid proceeded smoothly (≈80%) but a substantial amount of the rhamnose derivatives decomposed giving lower yields (35-50%). At no time could any racemisation of the α-chloropropionic acid or alkylation products be detected. Deprotection and purification gave the glycosides, methyl 6-O-[(R)- and (S)-1-carboxyethyl]-α;-D-galactopyranoside (1 and 2) and methyl 4-O-[(R)- and (S)-1-carboxyethyl]-α-L-rhamnoside as white solids.
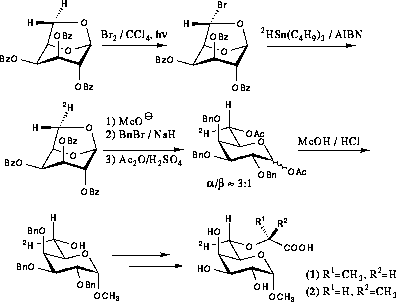
In order to make an unambiguous assignment of the H-6 protons stereospecifically deuterated derivatives were prepared (scheme 4.2). Photochemical bromination of 2,3,4-tri-O-benzoyl-1,6-anhydrogalactose resulted in the exchange of the exo-hydrogen on C-6, i.e. H-6proS, for bromine. After purification the bromide was subjected to radical mediated dehalogenation using tributyltin deuteride whereby deuterium was introduced with the same stereochemistry.89 After Zemplén deacetylation and benzylation the 1,6-anhydroring was opened by acetolysis giving a mixture of diacetates. Treatment of the diacetates with methanolic hydrogen chloride resulted in simultaneous deacetylation and Fischer glycosylation. After chromatographic separation the pure α-anomer could be obtained. The α-glycoside was then alkylated and deprotected as described for the undeuterated compounds.
Scheme 4.2 (paper IV)
Stereospecific deuteration

4.3 NMR studies

The assignment of the 1H-NMR signals of the rhamnose derivatives was straightforward using 1H,1H-COSY spectra and subsequently the 13C-signals using 13C,1H correlated spectra. The assignment of the spectra of compounds 1 and 2 was complicated by the close proximity of several 1H- as well as 13C-NMR resonances. The signal for C-6 could be assigned using DEPT experiments and this in turn allowed the assignment of the H-6 signals. In an attempt to resolve the remaining uncertainties a DIS 90 experiment was performed.
Normally spectra are recorded in D2O which causes a slight but noticeable isotope effect on the hydroxyl-bearing carbons and their neighbours. This isotope effect can be measured by comparing spectra recorded in D2O and in 80-90% H2O/D2O . By comparing the effects on methyl α-D-galactopyranoside with those on 1 and 2 the assignments for C-4 and C-5 of compound 2 could be determined. The diastereomeric hydroxymethyl protons could be assigned since the H-6proS resonances are absent in the deuterated compounds.
All four compounds showed typical substitution shifts in 13C-NMR (α-C downfield 7-10 ppm, β-C upfield 0.5-2.5 ppm). The effects on the 1H-NMR spectra were minor. The differences between the pairs of diastereomers were small and an assignment of configuration in a polysaccharide based on NMR only would be difficult.

4.4 Conformational analysis

The C5-C6 bond of hexopyranoses is known to be very flexible and by the substition at O6 two additional flexible bonds are introduced. Since the same degrees of freedom are present in 6-linked saccharides, such as dextran, and hence the same computational and experimental difficulties should be encountered, it was of interest to attempt to determine the conformations of 1 and 2.
The three exocyclic torsions are labelled φ' (H2'-C2'-O6-C6), ψ' (C2'-O6-C6-C5) and ω (O5-C5-C6-O6), respectively, in analogy with 6-linked disaccharides. Homo- and heteronuclear coupling constants were measured and interpreted using a three state model using limiting values for the staggered conformers from equations [1] and [2]. The conformation of the ω torsion was analysed using the JH5,H6 couplings as previously described 70 and the results were similar to those obtained for methyl α-D-galactopyranoside.
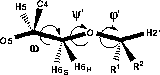
Degrees of Freedom
Table 4.1: Population of torsional states calculated from coupling constants using equations [1] and [2]. Values obtained from LD are given in parenthesis.
Pg+ Pt Pg-
1 φ' -a (30) 40 (2) -a (68)
ψ' 60 (14) 0 (68) 40 (18)
ω' 57 (68) 26 (25) 18 (7)
2 φ' -a (92) 32 (0) -a (8)
ψ' 55 (2) 0 (60) 45 (38)
ω' 62 (95) 26 (3) 12 (2)
Me α-D-Galp ω 47 39 14
a) Experimental data does not allow for the separate calculation of populations in the gauche states.
Heteronuclear couplings between the H6 protons and C2' were recorded and the analysis using a published Karplus-relationship 67 suggested the total absence of ψ'-trans conformers.
Across the φ'-torsion there is only one heteronuclear coupling that can be measured, that of H2' to C6. The values obtained both for 1 and 2 suggest that this torsion is about one third trans, as would be expected in the absence of any strong conformational preference (table 4.1). Although the rotamer population distributions should be similar to those calculated from the coupling constants, it must be kept in mind that the accuracy of Karplus equation for 3JCH is significantly lower than that for 3JHH as the former was developed for glycosidic linkages and does not take electronegativity effects into account. 91 Coupling constants alone do not provide any information as to the mutual dependence of the individual torsions. Such information could be available from NOE measurements but this requires well resolved resonances. Although calculated populations for 1 and 2 are very similar the measured differences in coupling constants are significant.
Table 4.2: Measured coupling constants Calculated values obtained from LD using equations [1] and [2] are given in parenthesis.
JH5,H6R JH5,H6S JH6S,C2' JH6R,C2' JC6,H2'
1 7.1 4.6 3.7 4.9 3.7
(7.7) (3.8) (2.7) (2.9) (3.1)
2 7.6 4.6 4.2 4.8 3.3
(9.7) (1.5) (2.8) (3.2) (2.6)
Me α-D-Galp70 7.8 6.0
The potential energy surfaces obtained from grid searches for 1 and 2 were found to be similar. Three 10 ns Langevin dynamics simulations were performed for each isomer. The population distributions from different runs were similar indicating that conformational space is well sampled. The trajectories were analysed both as population distributions between different torsional states as well as conformers defined by combinations of the three torsion angles. Coupling constants were calculated from the trajectories using equations [1] and [2].
3JHH= P1cos2θ+ P2cos θ+ P3+ ΣΔχi{ P4+P5cos2 (ζθ+P4|Δχi|)} [1]92
where P1-P6 are constants, Δχi the relative electronegativities (rel. to H) of the substituents, ζ a constant depending on the orientation of a substituent and θ the H-H-torsion angle.
3JCOCH= 5.7cos2θ-0.6cos θ+0.5 [2]67
The simulations show that the conformational space occupied by 2 is more restricted than that for 1 and there are only two conformers with significant populations whereas 1 has five. Compound 2 also has a much larger population in the g+ state of ω than what is compatible with experiment. All backcalculated homo- and heteronuclear coupling constants showed significant differences from the experimental values for both 1 and 2. Only the ω populations calculated from the simulation of 1 are in good agreement with those obtained from experiment and this despite the fact that the calculated couplings themselves are significantly different from the experimental ones.

4.5 Results

In both diastereomers high flexibility is indicated by experiment as well as simulation. The energy difference between different populated conformations in the simulations is small (≤1.1 kcal) and the outcome can therefore be expected to be sensitive to small changes in the force field. Considering the very shallow energy surface it is not surprising that the overall agreement with the solution structure is poor. The agreement between the crystal structure of 193 and simulation is, however, good. The solid state structure has φ', ψ' and ω values of -35 °, 171 ° and 77 °, respectively, to be compared with -50 °, 178 ° and 66 ° in the most highly populated conformation in the LD simulations. This is to be compared with the NMR derived structure in which this conformation is not populated. Thus, the solid state and solution structures of 1 are different and the structure from simulation is intermediate, showing features from both. Whether this is a peculiarity of this simulation or if it might be an inherent feature of the CHARMM force field is not known. It is likely that the differences between physical states are more accentuated in flexible molecules like these and therefore differences between solid state, solution and vacuum (simulation) may be anticipated.
Last update: Jun 24, 2009 :: Editor :: Webmaster :: Valid XHTML 1.0 Strict :: Valid CSS